The Brain Activity Flow ("Actflow") Toolbox

Version 0.3.1


View on GitHub


Overview

This toolbox facilitates linking brain connectivity with task-evoked activity and associated cognitive/behavioral functions. The primary focus is on activity flow modeling and related methods (Cole et al. (2016) & Ito et al. (2022)).

Activity flow modeling is based on core principles underlying neural network modeling, applying these principles to empirical neural/neuroimaging data. The core theoretical construct is that of activity flow — the movement of activity between neural populations. Activity flow modeling is a highly flexible framework that is constantly being improved via better connectivity methods and creative uses of the approach to better understand brain function.

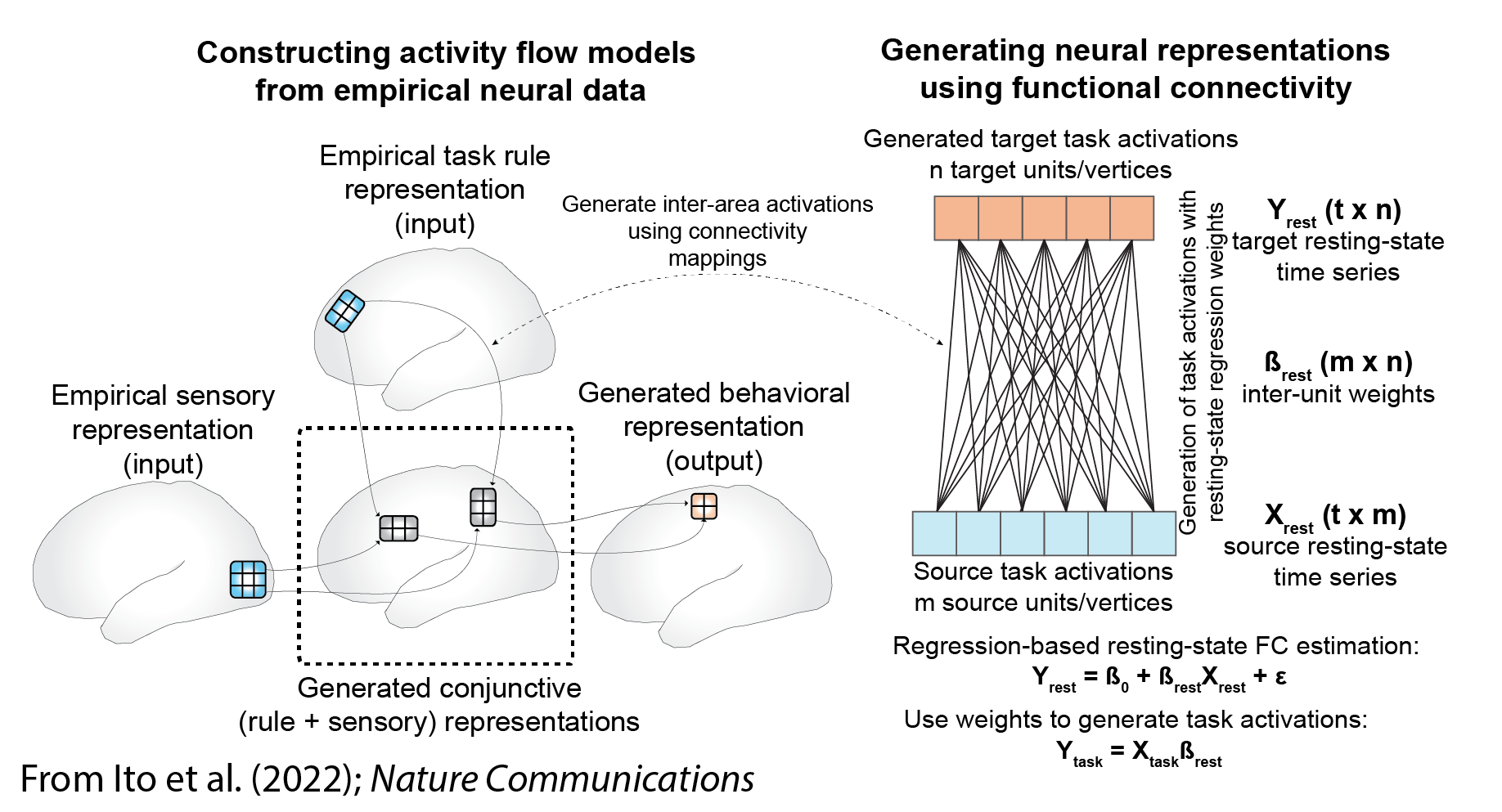
Activity flow modeling can be used, for instance, to infer whether one or more brain connections are involved in producing a particular function. This method can also be used to relate multiple task-evoked activations to each other (e.g., predicting one neural population's activity from another's activity). More generally, activity flow modeling can be thought of as creating network coding models (Ito et al. (2020)), which are empirically-constrained neural network models.

Other methods included in the toolbox (which can optionally be used along with activity flow modeling) are advanced versions of resting-state functional connectivity and task-state functional connectivity. The primary focus (for now) is on fMRI data, but in principle these approaches can be applied to any kind of neural data.

This code repository was created by the Cole Neurocognition Lab at Rutgers University: http://www.colelab.org/
We are happy for others to contribute to the code as well.

See the example notebook to see the Actflow Toolbox in action
We provide 30 subjects' data from the Human Connectome Project for trying out the toolbox.

For a more complete tutorial walkthrough of the toolbox see Cocuzza et al. (2022) STAR Protocols

Core algorithm and principles behind activity flow modeling

Activity flow modeling is a method validated and published in Nature Neuroscience in 2016 (see Cole et al. (2016)), with 14+ follow-up studies further validating the approach.

Activity flow modeling has two basic steps:

1) Activity flow modeling: Simulating the flow (movement) of activity between neural populations, using empirical data to estimate activity levels and routes of flow (connectivity). This is done by running the standard "propagation rule" and "activation rule" steps used in most neural network simulations (see Ito et al. (2020)). In the standard approach each neural population's activity level is predicted based on the flow from every other recorded neural population (from Cole et al. (2016)):

2) Testing prediction accuracy: The predicted brain activity pattern is compared to the actual recorded activity, providing evidence for or against the activity flow model used to make the predictions. Predictions of multiple models can be compared to quantify model validity. Two examples of predicted-to-actual accuracy testing with fMRI data (from Cole et al. (2016)):

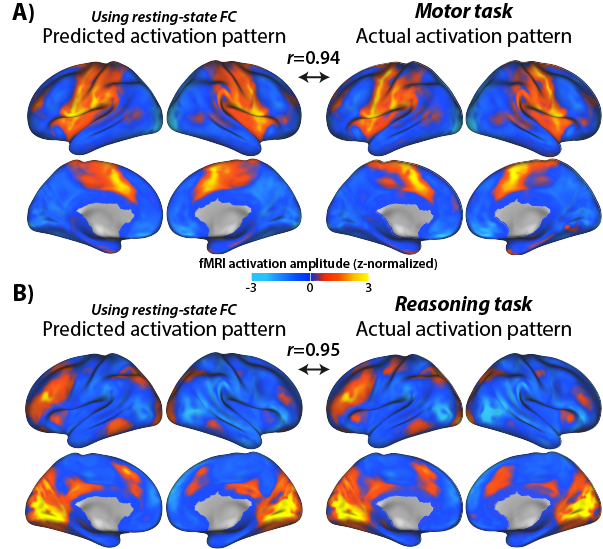
In principle, any measure of neural activity and any measure of neural connectivity (e.g., structural connectivity) can be used with activity flow modeling. Some modifications are necessary for fast temporal resolution data such as EEG/MEG or multi-unit recording, but these should be available soon (we are working on it!).

More background info on activity flow modeling can be found on an FAQ about the Cole et al. (2016) paper

Included connectivity modeling methods

Preprocessing

Cite as:

  1. Cole MW, Ito T, Bassett DS, Schultz DH (2016). "Activity flow over resting-state networks shapes cognitive task activations". Nature Neuroscience. 19:1718–1726. doi.org/10.1038/nn.4406
  2. https://colelab.github.io/ActflowToolbox/
    3. and
  3. The article that describes the specific toolbox functions being used in most detail

How to install

Option 1:
Within an Anaconda environment: conda install -c conda-forge actflow

Option 2:
pip install actflow

Option 3:
git clone --recurse-submodules git@github.com:ColeLab/ActflowToolbox.git

Email list/forum

We strongly encourage you to join the ColeNeuroLab Users Group (https://groups.google.com/forum/#!forum/coleneurolab_users), so you can be informed about major updates in this repository and others hosted by the Cole Neurocognition Lab.

Conventions

Examples

A Jupyter Notebook with example analyses (and example data) is viewable here: HCP_example.ipynb

Example of calculating activity flow mapping predictions using multiple-regression FC and standard task-evoked activations with fMRI data (in Python 3; assumes task activations and resting-state fMRI data are already loaded):

import ActflowToolbox as actflow
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

restFC_mreg=np.zeros((np.shape(restdata)[0],np.shape(restdata)[0],np.shape(restdata)[2]))
for scount in np.arange(np.shape(restdata)[2]):
    restFC_mreg[:,:,scount]=actflow.connectivity_estimation.multregconn(restdata[:,:,scount])

print("==Activity flow mapping results, multiple-regression-based resting-state FC, 24 task conditions==")
actflowOutput_restFCMReg_bycond = actflow.actflowcomp.actflowtest(activations_bycond, restFC_mreg)

Output:

==Activity flow modeling results, multiple-regression-based resting-state FC, 24 task conditions==
===Comparing prediction accuracies between models (similarity between predicted and actual brain activation patterns)===

==Comparisons between predicted and actual activation patterns, across all conditions and nodes:==
--Compare-then-average (calculating prediction accuracies before cross-subject averaging):
Each comparison based on 24 conditions across 360 nodes, p-values based on 30 subjects (cross-subject variance in comparisons)

Mean Pearson r = 0.78, t-value vs. 0: 62.27, p-value vs. 0: 1.9635597302245892e-32

Mean % variance explained (R^2 score, coeff. of determination) = 0.57

Mean MAE (mean absolute error) = 7.54

Note: Pearson r and Pearson r^2 are scale-invariant, while R^2 and MAE are not. R^2 units: percentage of the to-be-predicted data's unscaled variance, ranging from negative infinity (because prediction errors can be arbitrarily large) to positive 1. See https://scikit-learn.org/stable/modules/generated/sklearn.metrics.r2_score.html for more info.

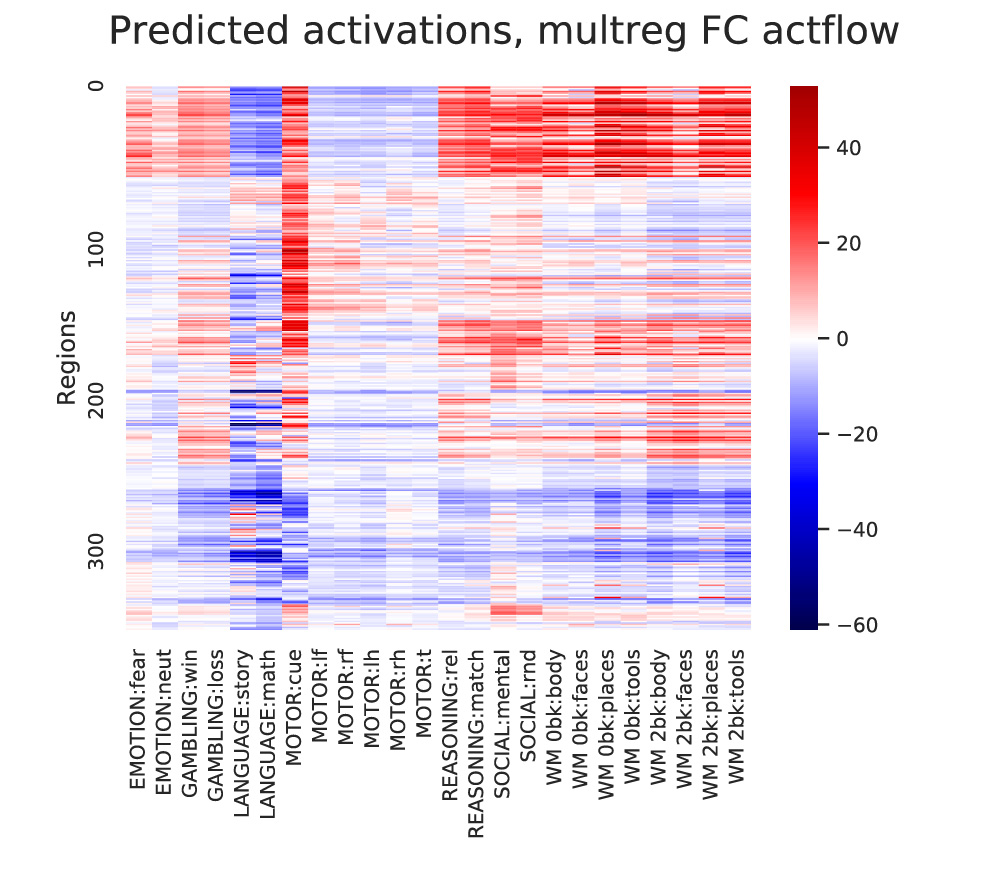
Visualizing the results:

#Visualize predicted and actual activation patterns, with multiple-regression FC
plt.figure(figsize=[7,5])
ax = sns.heatmap(np.mean(actflowOutput_restFCMReg_bycond['actPredVector_bytask_bysubj'],axis=2)[netorder,:],center=0,cmap='seismic',cbar=True,yticklabels=100,xticklabels=taskConditions)
ax.figure.suptitle('Predicted activations, multreg FC actflow')
ax.set(ylabel='Regions')

plt.figure(figsize=[7,5])
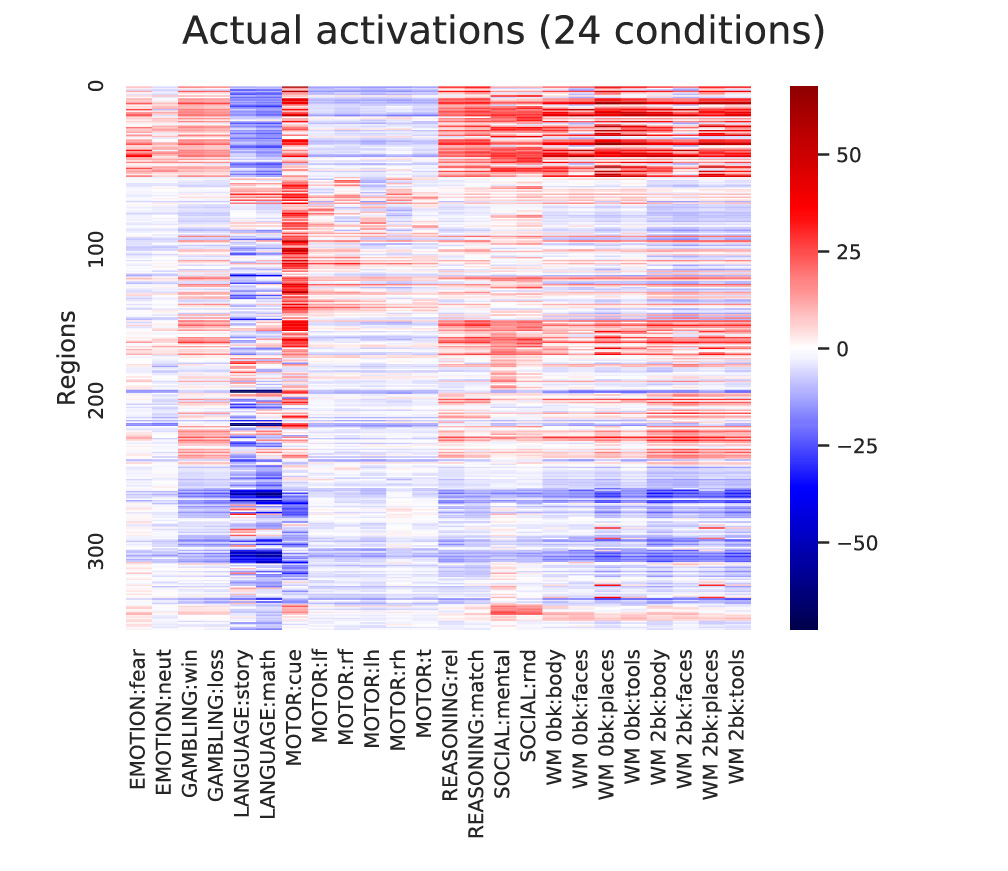
ax = sns.heatmap(np.mean(activations_bycond,axis=2)[netorder,:],center=0,cmap='seismic',cbar=True,yticklabels=100,xticklabels=taskConditions)
ax.figure.suptitle('Actual activations (24 conditions)')
ax.set(ylabel='Regions')

Output:

General guidelines for activity flow modeling

Software development guidelines

Publications that have used activity flow modeling and/or this toolbox

Using resting-state fMRI

Using task-state fMRI (often in addition to resting-state fMRI)

Using structural connectivity (diffusion MRI)

Using electroencephalography (EEG) or magnetoencephalography (MEG)